Original:http://www.xnumber.com/xnumber/mechanical1.htm
Часть I
Эпоха полиматов
«Недостойно, когда превосходные люди теряют часы, как рабы, в расчете на труд, который был бы безопасно отчислен кому-либо другому, если бы машины использовались».
Готфрид Вильгельм фон Лейбниц – 1685
Введение
Цель этого документа – кратко описать наиболее распространенные не электронные вычислительные устройства в историческом контексте и создать источник ссылок на другие страницы в Интернете, связанные с этой темой. Путешествие начинается 2500 лет назад с Abacus и заканчивается 30 лет назад с введением первых электронных калькуляторов.
Чтобы облегчить загрузку, документ был разделен на три части: часть I описывает эволюцию вычислительных устройств вплоть до изобретения ступенчатого колеса Лейбница. В части II обсуждаются основные события XIX века, а в части III рассматривается развитие офисных машин до 1960-х годов, когда на рынке появились первые электронные калькуляторы.
Абак
Математические концепции и их дети, арифметические операции, считались в течение тысяч лет чистым интеллектуальным упражнением, которое не могло быть дублировано или выполнено искусственным артефактом. Даже Abacus, появившийся в Малой Азии 2500 лет назад и до сих пор используемый сегодня, является лишь устройством для помощи памяти, а не реальной вычислительной машиной.
Абак – это гениальное устройство подсчета, основанное на взаимном расположении двух наборов бисера, движущихся на параллельных струнах. Первый набор содержит пять бусинок на каждой строке и позволяет считать от 1 до 5, в то время как второй набор имеет только два шарика на строку, представляющие числа 5 и 10. Система Абак, по-видимому, основана на радиусе из пяти. Использование радикса из пяти имеет смысл, так как люди начали считать объекты на своих пальцах.
Калькулятор Antikythera
Когда-то, между 100 г. до н.э. и 65 г. до н.э., греческий корабль с грузом бронзовых и мраморных статуй и других артефактов из Родоса в Рим погрузился близко к побережью Антикитры, небольшого острова Греции. Он оставался на дне моря под 140 футами воды в течение двух тысячелетий, пока не был обнаружен в 1901 году местными дайверами-губками.
Остатки, хранящиеся в Национальном музее в Афинах, включают в себя механизм древнего механизма, ныне известный как Калькулятор Антикитера.
Это интересное устройство, состоящее из 32 зубчатых колес, напоминает механизм часов 18 века и использовалось для расчета движений Солнца и Луны.
Кости Нейпира
Еще одним интересным изобретением являются кости Нейпира, умный инструмент умножения, изобретенный в 1617 году математиком Джоном Нейпиром (1550-1617) из Шотландии.
Кости представляют собой набор вертикальных прямоугольных стержней, каждый из которых разделен на 10 квадратов. Верхний квадрат содержит цифру, а остальные квадраты содержат первые 9 кратных цифр. Каждый кратный имеет свои цифры, разделенные диагональной линией. Когда число строится путем расположения бок о бок стержней с соответствующими цифрами сверху, то его кратное можно легко получить, читая соответствующую строку кратных слева направо, добавляя цифры, найденные на параллелограммах, образованных диагональю Линий. Неудивительно, что Джон Нейпир также изобретатель логарифмов, понятие, используемое для изменения умножения в дополнение.
Кости Нейпира были очень успешными и широко использовались в Европе до середины 1960-х годов.
Логарифмы были также основанием для изобретения правила скольжения Уильямом Огтредом (1574-1660), Англии, в 1633 году.
Дизайн Леонардо да Винчи
Природа имеет бесчисленные примеры механических решений практических задач, поэтому неудивительно, что первую попытку спроектировать вычислительную машину, вероятно, сделал мастер машинных артефактов Леонардо да Винчи (1452-1519).
Многие из его гениальных идей Леонардо да Винчи получили благодаря тщательному наблюдению механиков, участвующих в движении живых организмов. Интересно, что природа не развивала колесо как решение этой проблемы; Это решение было оставлено для человеческой изобретательности. Интересно отметить, что колесо было базой для большинства механических устройств, используемых для репликации мыслительного процесса, участвующего в арифметических операциях. Джордж Чейз (George Chase) сказал: «История механических вычислительных машин по своей сути – это история цифрового колеса и устройств, которые вращают его, чтобы регистрировать цифровые и десятизначные значения».
Машина Шикарда
Первые вычислительные машины были построены талантливыми математиками, движимыми сильным желанием упростить повторяющийся характер арифметических операций.
Первая известная расчетная машина была изготовлена Вильгельмом Шикардом (1592-1635). В 1623 году Шикард, ученый, а затем профессор в Тюбингенском университете в Вюртемберге, ныне входящем в состав Германии, разработал и построил механическое устройство, которое он назвал «Расчетные часы». Способный добавлять и вычитать до шестизначных чисел, артефакт был основан на движении шести зубчатых колес, направленных через «искалеченное» колесо, которое с каждым полным оборотом позволяло колесу, расположенному справа, поворачивать 1/10 полного очередь. Механизм переполнения позвонил. Функция добавления была разработана, чтобы помочь выполнять умножение с набором цилиндров Нейпира, включенным в верхнюю половину машины. Согласно его записям, прототип этой машины был уничтожен пожаром. Похоже, в то время существовал еще один прототип, но он так и не был найден.
Друг великого астронома Иоганна Кеплера (1571-1630), Шикард отправил ему несколько писем в 1623 и 1624 гг., Кратко описывая его изобретение. Schickard и его семья не пережили бубонной чумы, и его подробные заметки оставались неизвестными, пока не были обнаружены в 1935 и 1956 годах историком Францем Хаммером. Математик Бруно фон Фрейтаг из Тюбингенского университета использовал их для реконструкции машины в 1960 году. Одна единица находится в Немецком музее в Мюнхене.
Паскалин
Блез Паскалю (1623-1662) было только 18 лет, когда он задумал Паскалина в 1642 году. Будучи ранним французским математиком и философом, Паскаль обнаружил в возрасте 12 лет, что сумма углов в треугольнике всегда равна 180 градусам. Позже он заложил основы теории вероятностей и внес значительный вклад в науку о гидравлике. Pascaline, построенный в 1643 году, возможно, был первым механическим добавочным устройством, фактически используемым для практических целей. Он был построен Паскалем, чтобы помочь своему отцу, Этьену Паскалю, сборщику налогов, с утомительной деятельностью по добавлению и вычитанию больших последовательностей чисел. Однако машина была трудна в использовании и, вероятно, не очень полезна из-за французской денежной системы, которая не была базой 10. У ливров было 20 золей, а у золя было 12 денье.
Паскаль не был знаком с машиной Шикарда, и его решение было не таким элегантным и эффективным. Как сказал Пол Дюна, «если идеи Шикарда нашли широкую аудиторию, то машина Паскаля не была бы изобретена».
Он был построен на латунной прямоугольной коробке, где набор зубчатых циферблатов перемещал внутренние колеса таким образом, что полное вращение колеса вызывало колесо слева, чтобы продвинуться на один десятый. Хотя первый прототип состоял всего из 5 колес, более поздние были построены с 6 и 8 колесами. Для вращения циферблатов использовался штифт. В отличие от машины Шикарда, колеса двигались только по часовой стрелке и предназначались только для добавления номеров. Вычитание осуществлялось с применением громоздкой техники, основанной на добавлении девятого дополнения.
Хотя машина привлекла к себе большое внимание в те дни, она не получила широкого признания, потому что она была дорогой, ненадежной, а также трудной в использовании и производстве. К 1652 году было изготовлено около 50 единиц, но продано менее 15 единиц. Первоначально Паскаль очень интересовался своим изобретением, и даже получил «привилегию» (средневековый эквивалент патента) за свою идею в 1649 году, но его интерес к науке и «материальным» занятиям закончился, когда он отступил к Янсенсисту Монастырь в 1655 году сосредоточил все свое внимание на философии. Он умер в 1662 году.
В течение 30 лет после изобретения Паскаля несколько человек построили вычислительные машины на основе этого проекта. Самым печально известным был добавочный аппарат сэра Сэмюэля Морланда (1625-1695) из Англии. Эта машина, изобретенная в 1666 году, имела двенадцатеричную шкалу, основанную на английской валюте, и потребовала вмешательства человека, чтобы ввести перенос, отображаемый на вспомогательном циферблате.
Интересно отметить, что даже в начале 20-го века несколько компаний представили модели, основанные непосредственно на дизайне Паскаля. Одним из примеров является Lightning Portable Adder, представленный в 1908 году компанией Lightning Adding Co. из Лос-Анджелеса. Другим примером является Addometer, введенный в 1920 году надежной машиной и Adding Machine Co. из Чикаго. Ни один из них не достиг коммерческого успеха.
Лейбниц Ступенчатый барабан
Это было в 1672 году, когда знаменитый немецкий ученый, математик и философ Готфрид Вильгельм фон Лейбниц (1646-1716), со-изобретатель дифференциального исчисления, решил построить машину, способную выполнять четыре основные арифметические операции. Он был вдохновлен устройством подсчета шагов (шагомер), которое он видел во время дипломатической миссии в Париже.
Как и Паскаль, Лейбниц был вундеркиндом. Он изучил латынь к восьми годам и получил вторую докторскую степень, когда ему было 19. Как только он узнал о дизайне Паскаля, он впитал в себя все свои детали и улучшил дизайн, чтобы учесть умножение и деление. К 1674 году его проект был завершен, и он заказал здание прототипа мастеру из Парижа по имени Оливье.
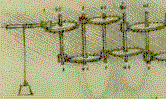
Stepped Reckoner, как Лейбниц называл свою машину, использовал специальный тип снаряжения, называемый ступенчатым барабаном или колесом Лейбница, который представлял собой цилиндр с девятью стержнеобразными зубцами, увеличивающими длину, параллельную оси цилиндра. Когда барабан вращается с помощью кривошипа, обычное десятицилиндровое колесо, закрепленное на скользящей оси, поворачивается от нуля до девяти позиций в зависимости от его относительного положения к барабану. Как и в устройстве Pascal, для каждой цифры имеется один набор колес. Это позволяет пользователю перемещать мобильную ось так, что когда барабан вращается, он генерирует в обычных колесах движение, пропорциональное их взаимному положению. Затем это движение преобразуется устройством в умножение или деление в зависимости от направления вращения ступенчатого барабана.
Нет никаких доказательств того, что когда-либо было сделано более двух прототипов этой машины. Несмотря на то, что Лейбниц был одним из самых выдающихся эрудитов своего времени, он умер в нищете и без награды. Его машина оставалась на чердаке Университета Геттингена, пока рабочий не обнаружил ее в 1879 году, исправляя утечку в крыше. Сейчас он находится в Государственном музее Ганновера; Другой – в Немецком музее в Мюнхене.
Расчетные устройства в XVIII веке
Проекты Паскаля и Лейбница были основой большинства механических калькуляторов, построенных в XVIII веке. Джованни Полени сделал одно в 1709 году, Лепин в 1725 году, Антониус Браун в 1725 году, Якоб Леупольд в 1727 году, Хиллерин де Бойстиссандау в 1730 году, К.Л. Герстена в 1735 году, Иакова Исаака Перейра в 1750 году, Филиппа Матье Хана в Германии в 1773 году. Чарльз, третий граф Стэнхоуп, в Англии, в 1775 году; Йохан Хелфрейх Мюллер в 1783 году, Яков Ох в 1790 году и Рейххолд в 1792 году. [4].
Особое внимание заслуживает парсон Филипп Матье Хаан (1730-1790), который разработал в 1773 году первый функциональный калькулятор на основе ступенчатого барабана Лейбница. Калькулятор Хана имел набор из 12 барабанов в круговом расположении, приводимом в действие рукояткой, расположенной на оси устройства. Хан производил эти машины до своей смерти в 1790 году, однако его два сына и его шурин Иоганн Кристофер Шустер продолжали производство, вероятно, в 1820 году.
К концу 18-ого столетия вычислительные машины были все еще раритетами, используемыми для целей показа, а не для фактического использования. Ограничения, накладываемые технологией, сделали невозможным встретить мечту Паскаля о том, чтобы сделать их практичным вычислительным устройством.